【第4回垂れ流し数学模試】文型第1問解説

皆さんこんにちは!
TomoKです。

今回は 第4回垂れ流し数学模試 の 文型第1問(1)(2) を解説しようと思います。

文型　第1問(1)

問題

自然数を1から順に, 10進数による最上位から順に書き並べてできる数列 \[1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 0, 1, 1, 1, 2, 1, 3, 1, 4, \cdots\] について, 初項から第2022項までの総和はいくらか.

---

問題としては群数列の考えを用いた問題になります。
ただし, 群を使うまでもなく, 自然数の桁数や位の循環をうまく使うことで解くことができると思います。

解答のために考えること

まず数列の第2022項, すなわち1から順番に書いた時の2022番目の数字が, どの自然数の何の位になるのかを求めます。

和を求める計算は群のまとまりを意識して、たとえば一の位・十の位・百の位ごとに足したり、
あるいは桁数が1桁のものの和, 2桁のものの和, 3桁のものの和という具合に分けて計算するとよいと思います。

解答

自然数を1から順にある自然数$n$まで, 10進数における最上位から順に書いていった場合,
1から9までだと1桁なので, それまでに書く数字の個数は9個.

また, 10から99までは2桁なので, 1から99までに書く数字の個数は
$9+2\times(99-10+1)=189$個,
100から999までは3桁なので, 1から999までに書く数字の個数は
$189+3\times(999-100+1)=2889$個である.

よって, この数列の第2022項, つまり上の書き方によって1から$n$まで書くときに
2022個目の数字を書くのは$n$が3桁の時で,
$2022-189=1833$を3でわった商は611, 余りは0なので,
2022個目に書く数字は$99+611=710$の一の位の0にあたる.

数列の初項から第2022項までの和は, 1から710までの自然数を順に書いた時に,
書く1個1個の数字を全て足した和に等しい.

書く自然数は, 一の位が1, 2, …, 9, 0の順に循環しており, これらの和は$1+2+\cdots+9+0=45$
これが$71+1=712$回循環するので, 一の位すべての和は$45\times 71=3195$

次に十の位は, 1つ変わる度に一の位が0, 1, …, 9の10個分あり,
十の位の0, 1, …, 9の循環が$6+1=7$回と, 700から710までの十の位を合わせて,
十の位すべての和は$(0+1+\cdots+9)\times 7\times 10+0\times 10+1=3151$

百の位は, 1つ変わるたびに下2桁が00, 01, …, 99の100個分あり,
その100個分がすべてそろう, 百の位が1,2,3,4,5,6の場合に,
700から710までの百の位を合わせて,
百の位すべての和は$(1+2+3+4+5+6)\times 100+7\times 11=2177$

したがって, 数列における初項から第2022項までの和は, \[3195+3151+2177=\bold{8523} \]

なお、総和を桁数ごとに求める場合は,

• 1桁の自然数の各位の総和は $1+2+\cdots +9=45$
• 2桁の自然数の各位の総和は, 一の位の$0+1+2+\cdots +9=45$が9個,
  十の位は1つにつき一の位が0から9までの10個で, 十の位自体も1から9まで動くので,
  $1+2+\cdots +9=45$が10個
  合わせて, $45\times(9+10)=835$
• 3桁の自然数のうち, 699までの各位の総和は, 下2桁分は$45+835=900$が6個,
  百の位はは1つにつき下二桁が00から99までの100個で, 百の位は1から6まで動くので,
  $1+2+3+4+5+6=21$が100個
  また700から710までの各位の総和は, 百の位は7が11個, 十の位は1が1個のほかはすべて0,
  一の位は$0+1+2+\cdots +9+0=45$
  よって, 3桁の自然数の各位の総和は, $900\times 6+21\times 100+7\times 11+1+45=7623$

よって全部合わせて, $45+835+7623=8523$と出すことができます.

いずれにしても, まとまりがいくつか考えられるので, それをうまく使うことで計算していけば難しくはないでしょう.

---

文型　第1問(2)

問題

${\rm AB}={\rm AC}=1$かつ$\angle{\rm A}$が鈍角である二等辺三角形ABCがあり,
その重心をG, 外心をOとすると, G, Oが辺BCに関して対称であるという.

このとき, 辺BCの長さを求めよ.

平面図形の問題です.
重心や外心の性質, および辺BCに関しての対称性をうまく使えば, こちらも難しくはないでしょう.

解答のために考えること

AGとBCの交点をM, $\triangle{\rm ABC}$の外接円の半径を$R$と置いて,
OM, AM, BMを$R$を用いて表してみましょう.

解答

Gは$\triangle{\rm ABC}$の重心だから, AGとBCの交点をMとすれば${\rm BM}={\rm CM}$
これと${\rm AB}={\rm AC}$より$\angle{\rm AMB}$は直角であるから, Oは直線AG上にある.

またOは$\triangle{\rm ABC}$の外心なので, $\triangle{\rm ABC}$の外接円の半径を$R$とすれば,
${\rm OA}={\rm OB}={\rm OC}=R$

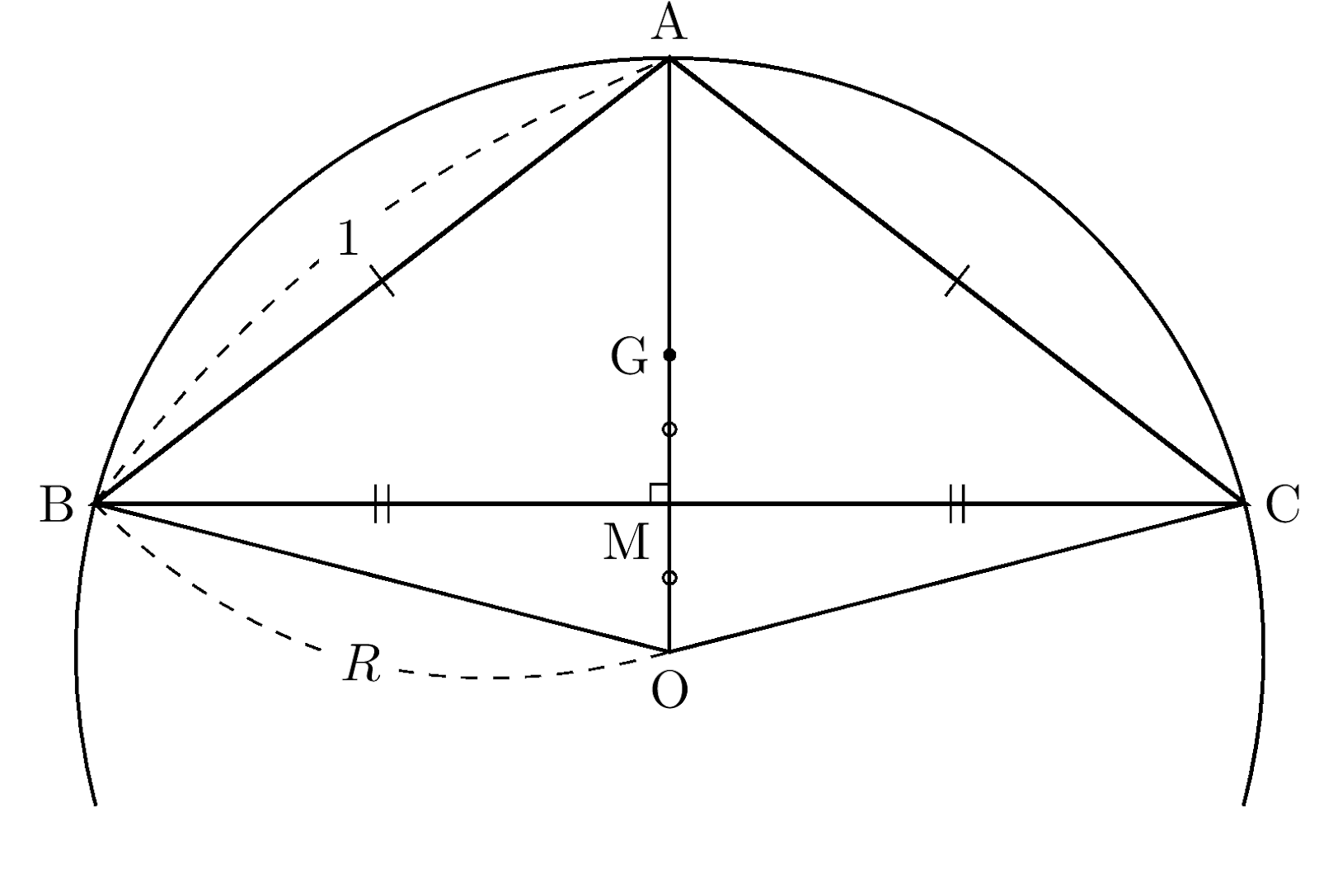
G, Oが辺BCに関して対称であることと${\rm AG}:{\rm GM}=2:1$より, ${\rm AG}:{\rm GM}:{\rm MO}=2:1:1$

よって${\rm MO}=\dfrac{1}{4}R$であるので, $\triangle{\rm BMO}$で三平方の定理を用いて, \[{\rm BM}=\sqrt{{\rm OB}^2-{\rm OM}^2}=\sqrt{R^2-\left(\dfrac{1}{4}R\right)^2}=\dfrac{\sqrt{15}}{4}R\]

${\rm AM}=\dfrac{3}{4}R$であるから, $\triangle{\rm AMB}$で三平方の定理を用いて, \[\begin{aligned} {\rm AB}&=\sqrt{{\rm AM}^2+{\rm BM}^2}=\sqrt{\left(\dfrac{3}{4}R\right)^2+\left(\dfrac{\sqrt{15}}{4}R\right)^2}=\dfrac{\sqrt{6}}{2}R\\ &=1 \end{aligned}\] よって, $R=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}$

以上より, \[{\rm BC}=2{\rm BM}=2\cdot\dfrac{\sqrt{15}}{4}\cdot\dfrac{\sqrt{6}}{3}=\bold{\dfrac{\sqrt{10}}{2}}\]

重心と外心の性質を正しく使えば, 三平方の定理との合わせ技で難なく解くことができるかと思います.

次回は文型第2問解説です。 理系の問題はその次の記事にて第2問(文型第3問)を解説します。

それでは、最後までお読みいただき、ありがとうございました。
ではまた。