【第5回垂れ流し数学模試】理型第5問解説

皆さんこんにちは!
TomoKです。

今回は 第5回垂れ流し数学模試 の 理型第5問 を解説しようと思います。

理型　第5問

問題

底面円の半径が1, 高さが4の直円柱Aについて, 2つの底面円の中心をそれぞれ$\rm O$, $\rm O'$とし, 底面円Oの周上に点Pをとる.
また, 線分$\rm OO'$の中点をMとする.

直円柱Aを直線PMを軸として回転させるとき, 直円柱Aの表面が通過する領域の体積を求めよ.

解答のために考えること

直線PMを軸にして回転させたときの体積なので,
できる立体を軸に垂直に切った時の断面積を積分していきます.
断面積は同心円となりますので, 回転前の直円錐Aの表面の, 同じ平面による断面(曲線になるはず)上の点Qと
直線PMとの距離のとりうる範囲を考えれば, 断面積が分かります.

場合分けが3つに分かれ, 計算が面倒ですが, 根気良く進めていきましょう.

解答

Aの表面が回転によって通過する領域を$D$,
$D$のうち, Mを通りPMに垂直な平面に関して, その平面を含みPと同じ側にある領域を$D_1$,
$D$, $D_1$の体積をそれぞれ$V$, $V_1$とする.

直円柱AがMに関して点対称であることより, $D$もMに関して点対称である.
したがって$V=2V_1$であるので, 以下で$V_1$を求める.

線分PM上に点Tをとり, ${\rm PT}=t$とおく.
Tを通り線分PMに垂直な平面$\alpha_t$と直円柱Aの表面が交わってできる曲線を$C_t$とする.
$D_1$の$\alpha_t$による断面は, $\alpha_t$上で$C_t$をTを中心に回転させたときの$C_t$の通過領域であり,
それはTを中心とする円もしくは同心円状となる. その面積を$S(t)$とおく.

1. $\alpha_t$が底面円Oと交わる場合
   

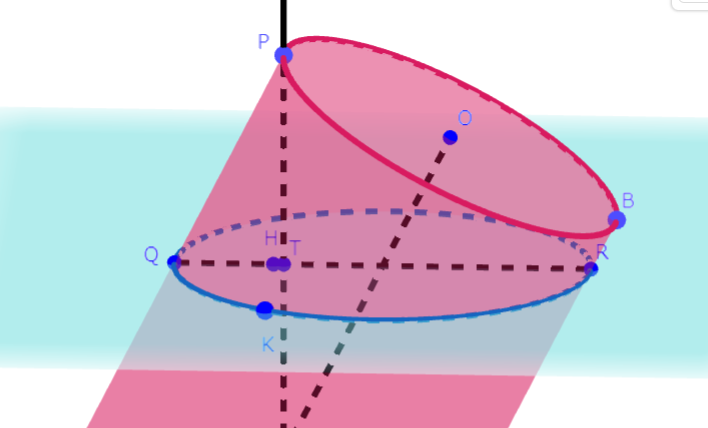
   $C_t$は左上の図のように, 直線部分と(直線でない)曲線部分からなる.
   ただし図の点R, Qはそれぞれ$C_t$の直線部分, 曲線部分と平面OPMとの交点である.

   直円柱Aの平面OPMによる断面は右上の図のような長方形PBCDであり,
   $\rm \triangle QTP∽\triangle PTR∽\triangle QPR∽\triangle PBC$,
   $\rm PB=2$, $\rm BC=4$, $\rm PC=\sqrt{2^2+4^2}=2\sqrt{5}$であることから,
   ${\rm TQ}=\dfrac{t}{2}$, ${\rm TR}=2t$, ${\rm QP}=\dfrac{\sqrt{5}}{2}t$, ${\rm PR}=\sqrt{5}t$である.
   $0\leqq {\rm PQ}\leqq 2$だから, $\alpha_t$が底面円Oと交わるのは$0\leqq t\leqq \dfrac{2}{\sqrt{5}}$ (…①)のときである.

   Kが$C_t$の曲線部分上にある場合, KからQRに下した垂線の足をH,
   線分QHの長さを$x$とおき, ${\rm KT}^2$を$t$および$x$で表す.

   

   底面円O上で, 点I, Jを, $\rm IK\jpara JH\jpara PQ$となるようにとると, Jは直線OPにあり,
   PQが底面円Oを含む平面に垂直だから, 四角形IKHJは長方形となる.
   ${\rm QH}:{\rm QR}={\rm PJ}:{\rm PR}$より$x:\dfrac{5}{2}t={\rm PJ}:\sqrt{5}t$, よって${\rm PJ}=\dfrac{2}{\sqrt{5}}x$である.
   よって${\rm OJ}=\left|\dfrac{2}{\sqrt{5}}x-1\right|$,
   ${\rm IJ}^2={\rm KH}^2=1^2-\left|\dfrac{2}{\sqrt{5}}x-1\right|^2=-\dfrac{4}{5}x^2+\dfrac{4}{\sqrt{5}}x$である.

   さらに, ${\rm HT}=\left|x-\dfrac{t}{2}\right|$だから, $$\begin{aligned} {\rm KT}^2&=-\dfrac{4}{5}x^2+\dfrac{4}{\sqrt{5}}x+\left|x-\dfrac{t}{2}\right|^2\\ &=\dfrac{1}{5}x^2+\left(\dfrac{4}{\sqrt{5}}-t\right)x+\dfrac{t^2}{4}\\ &=\dfrac{1}{5}\left(x+2\sqrt{5}-\dfrac{5}{2}t\right)^2-\dfrac{1}{5}\left(2\sqrt{5}-\dfrac{5}{2}t\right)^2+\dfrac{t^2}{4}\\ &=\dfrac{1}{5}\left(x+2\sqrt{5}-\dfrac{5}{2}t\right)^2-{t^2}+2\sqrt{5}t-4 \end{aligned}$$ よって①によって, Kが$C_t$の曲線部分にいる場合, つまり$0\leqq x\leqq \dfrac{5}{2}t$の場合,

   • ${\rm KT}^2$の最大は, $x=\dfrac{5}{2}t$のときに,
     $\dfrac{1}{5}\left(\dfrac{5}{2}t\right)^2+\left(\dfrac{4}{\sqrt{5}}-t\right)\cdot \dfrac{5}{2}t+\dfrac{t^2}{4}=-t^2+2\sqrt{5}t$
   • ${\rm KT}^2$の最小は, $x=0$のときに, $\dfrac{t^2}{4}$
   となり, これらの間の実数値をくまなくとる.

   Kが$C_t$の直線部分にいる場合は,
   ${\rm KT}^2$の最大は, $C_t$の曲線部分に$K$がいる場合で$x=\dfrac{5}{2}t$の場合に相当,
   また最小の場合はKがRにいるときだが, ${\rm TR}\gt{\rm TQ}$である.
   以上より, Kが$C_t$全体を動くときの${\rm KT}^2$最大・最小は,
   それぞれKが$C_t$の曲線部分にいる場合の最大・最小に一致する.

   したがって, $0\leqq t\leqq \dfrac{2}{\sqrt{5}}$の場合の$S(t)$は, $$S(t)=-t^2+2\sqrt{5}t-\dfrac{t^2}{4}=-\dfrac{5}{4}t^2+2\sqrt{5}t$$ となる.

2. $\alpha_t$が底面円Oと交わらない場合

   

   ${\rm PM}=\sqrt{5}$より$\dfrac{2}{\sqrt{5}}\leqq t\leqq \sqrt{5}$ (…②)である.

   この場合, 右の図のように$C_t$は1つの(直線部分のない)曲線でできているが,
   $C_t$は$t=\dfrac{2}{\sqrt{5}}$の時にできる曲線$C_{\frac{2}{\sqrt{5}}}$と合同である.
   よって${\rm QR}=\dfrac{5}{2}\cdot \dfrac{2}{\sqrt{5}}=\sqrt{5}$である.

   

   Kが$C_t$上にある場合, (i)と同様にKからQRへおろした垂線の足をH,
   ${\rm QT}=x$とおくとき,
   (i)の結果から, ${\rm KH}^2=-\dfrac{4}{5}x^2+\dfrac{4}{\sqrt{5}}x$, ${\rm HT}=\left|x-\dfrac{t}{2}\right|$は変わらないので,
   ${\rm KH}^2=\dfrac{1}{5}x^2+\left(\dfrac{4}{\sqrt{5}}-t\right)x+\dfrac{t^2}{4}=\dfrac{1}{5}\left(x+\dfrac{2}{\sqrt{5}}-\dfrac{t}{2}\right)^2-{t^2}+2\sqrt{5}t-4$
   も変わらない.

   したがって, $0\leqq x\leqq \sqrt{5}$と②から, Kが$C_t$上にある場合について,

   • ${\rm KT}^2$の最大は, $-\dfrac{2}{\sqrt{5}}+\dfrac{t}{2}\lt\dfrac{\sqrt{5}}{2}$を満たすことから,
     $x=\sqrt{5}$のときに, $\dfrac{1}{5}\cdot (\sqrt{5})^2+\left(\dfrac{4}{\sqrt{5}}-t\right)\cdot \sqrt{5}+\dfrac{t^2}{4}=\dfrac{t^2}{4}-\sqrt{5}t+5$
   • ${\rm KT}^2$の最小は,
     $-\dfrac{2}{\sqrt{5}}+\dfrac{t}{2}\leqq 0$すなわち$\dfrac{2}{\sqrt{5}}\leqq t\leqq \dfrac{4}{\sqrt{5}}$の場合には, $x=0$のとき, $\dfrac{t^2}{4}$
     $\dfrac{4}{\sqrt{5}}\leqq t\leqq \sqrt{5}$の場合には, $x=-\dfrac{2}{\sqrt{5}}+\dfrac{t}{2}$のとき, $-{t^2}+2\sqrt{5}t-4$

   となり, いずれの場合も最大値と最小値の間の実数値をくまなくとる.

   よって, $S(t)$は, $$\begin{array}{ll} \dfrac{2}{\sqrt{5}}\leqq t\leqq \dfrac{4}{\sqrt{5}}のときは, & S(t)=\dfrac{t^2}{4}-\sqrt{5}t+5-\dfrac{t^2}{4}=-\sqrt{5}t+5 \\ \dfrac{4}{\sqrt{5}}\leqq t\leqq \sqrt{5}のときは, & \begin{aligned}[t]S(t)&=\dfrac{t^2}{4}-\sqrt{5}t+5-\left(-{t^2}+2\sqrt{5}t-4\right)\\&=\dfrac{5}{4}t^2-3\sqrt{5}t+9=\left(\dfrac{\sqrt{5}}{2}t-3\right)^2\end{aligned} \end{array}$$

以上(i), (ii)より, $$\begin{aligned} V_1&=\dint_{0}^{\sqrt{5}}S(t) dt\\ &=\dint_{0}^{\frac{2}{\sqrt{5}}}\left(-\dfrac{5}{4}t^2+2\sqrt{5}t\right) dt + \dint_{\frac{2}{\sqrt{5}}}^{\frac{4}{\sqrt{5}}}\left(-\sqrt{5}t+5\right) dt + \dint_{\frac{4}{\sqrt{5}}}^{\sqrt{5}}\left(\dfrac{\sqrt{5}}{2}t-3\right)^2 dt\\ &=-\dfrac{5}{12}\left[t^3\right]_{0}^{\frac{2}{\sqrt{5}}}+\sqrt{5}\left[t^2\right]_{0}^{\frac{2}{\sqrt{5}}} -\dfrac{\sqrt{5}}{2}\left[t^2\right]_{\frac{2}{\sqrt{5}}}^{\frac{4}{\sqrt{5}}}+5\left[t\right]_{\frac{2}{\sqrt{5}}}^{\frac{4}{\sqrt{5}}} +\dfrac{2}{3\sqrt{5}}\left[\left(\dfrac{\sqrt{5}}{2}t-3\right)^3\right]_{\frac{4}{\sqrt{5}}}^{\sqrt{5}}\\ &=-\dfrac{2\sqrt{5}}{15}+\dfrac{4\sqrt{5}}{5}-\dfrac{6\sqrt{5}}{5}+2\sqrt{5}+\dfrac{7\sqrt{5}}{60}\\ &=\dfrac{19\sqrt{5}}{12} \end{aligned}$$

よって, $V=2V_1=\bold{\dfrac{19\sqrt{5}}{6}}$

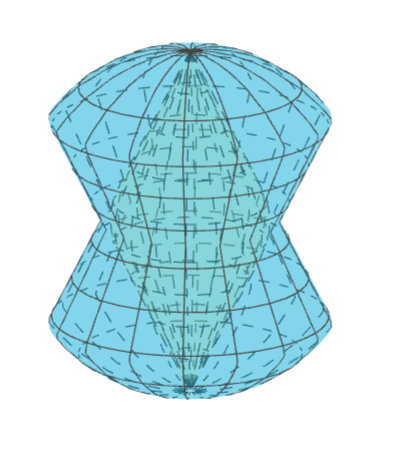
ちなみに、今回できる立体は, 左下の図のような形で,
外側の青い曲面で囲まれた立体から, 内側の黄色い局面をとり除いた形になります。
もとの円柱Aを合わせると、ちょうどAの底面や側面にピッタリ合っていることがわかると思います。

次回はラスト、理型第6問・文型第5問解説です。

それでは、最後までお読みいただき、ありがとうございました。
ではまた。