【第5回垂れ流し数学模試】文型第4問解説

皆さんこんにちは!
TomoKです。

今回は 第5回垂れ流し数学模試 の 文型第4問 を解説しようと思います。

この問題の(1), (2)で、$a$の範囲に誤りがありました。
(誤) (1) $0\lt a\leqq 1$のとき,... (2) $1\lt a$のとき,...
(正) (1) $0\lt a\leqq \dfrac{1}{2}$のとき,... (2) $\dfrac{1}{2}\lt a$のとき,...
以下は問題を修正した場合の解答になります。

文型　第4問

問題

$a$を正の定数とする.
$xy$座標平面上で, 曲線$y=x^2$の$-a\leqq x\leqq a$の部分を$C$とする.
1辺の長さが$1$の正方形$K$が$xy$座標平面上を, $K$のある1辺が$x$軸に平行になるように,
かつ$K$の2本の対角線の交点が$C$上にあるように動く.
正方形$K$の周および内部が通過しうる領域の面積を$S(a)$とする.

1. $0\lt a\leqq \dfrac{1}{2}$のとき, $S(a)$を$a$で表せ.
2. $\dfrac{1}{2}\lt a$のとき, $S(a)$を$a$で表せ.

解答のために考えること

積分を用いて面積を求めますが, $K$の通過する範囲を正しく図示する必要があります.
ただし動く範囲は, $K$の各頂点が$C$を平行移動した放物線上を動くことに気を付けると,
込み入った議論をせずに図がかけます.
(もちろん, 以下ではちゃんと議論をして通過領域を求めます.)

積分は放物線のほか, 何本かの直線に囲まれていますので,
工夫して求めていきましょう.

解答

まず, 点$(X, Y)$が$K$の通過領域上に存在するための必要十分条件は,

ある$-a\leqq t\leqq a$が存在して, $t-\dfrac{1}{2}\leqq X\leqq t+\dfrac{1}{2}$かつ$t^2-\dfrac{1}{2}\leqq Y\leqq t^2+\dfrac{1}{2}$

である.

ここで, $t-\dfrac{1}{2}\leqq X\leqq t+\dfrac{1}{2}$は$X-\dfrac{1}{2}\leqq t\leqq X+\dfrac{1}{2}$であるので,
これを満たす$X$に対し, $X-\dfrac{1}{2}$, $X+\dfrac{1}{2}$および$0$との大小によって, $Y$の範囲は以下のようになる.

1. $X+\dfrac{1}{2}\lt 0$すなわち$X\lt -\dfrac{1}{2}$のとき,
   $\left(X+\dfrac{1}{2}\right)^2-\dfrac{1}{2}\leqq Y\leqq \left(X-\dfrac{1}{2}\right)^2+\dfrac{1}{2}$
2. $X-\dfrac{1}{2}\lt -\dfrac{1}{2}\lt 0\leqq X+\dfrac{1}{2}$すなわち$-\dfrac{1}{2}\leqq X\lt 0$のとき,
   $-\dfrac{1}{2}\leqq Y\leqq \left(X-\dfrac{1}{2}\right)^2+\dfrac{1}{2}$
   
3. $-\dfrac{1}{2}\leqq X-\dfrac{1}{2}\lt 0\leqq X+\dfrac{1}{2}$すなわち$0\leqq X\lt \dfrac{1}{2}$のとき,
   $-\dfrac{1}{2}\leqq Y\leqq \left(X+\dfrac{1}{2}\right)^2+\dfrac{1}{2}$
   
4. $0\leqq X-\dfrac{1}{2}$すなわち$\dfrac{1}{2}\leqq X$のとき,
   $\left(X-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\leqq Y\leqq \left(X+\dfrac{1}{2}\right)^2+\dfrac{1}{2}$
   

ただし, $-a\leqq t\leqq a$より,
$-a-\dfrac{1}{2}\leqq X\leqq a+\dfrac{1}{2}$かつ$-\dfrac{1}{2}\leqq Y\leqq a^2+\dfrac{1}{2}$である.

1. 

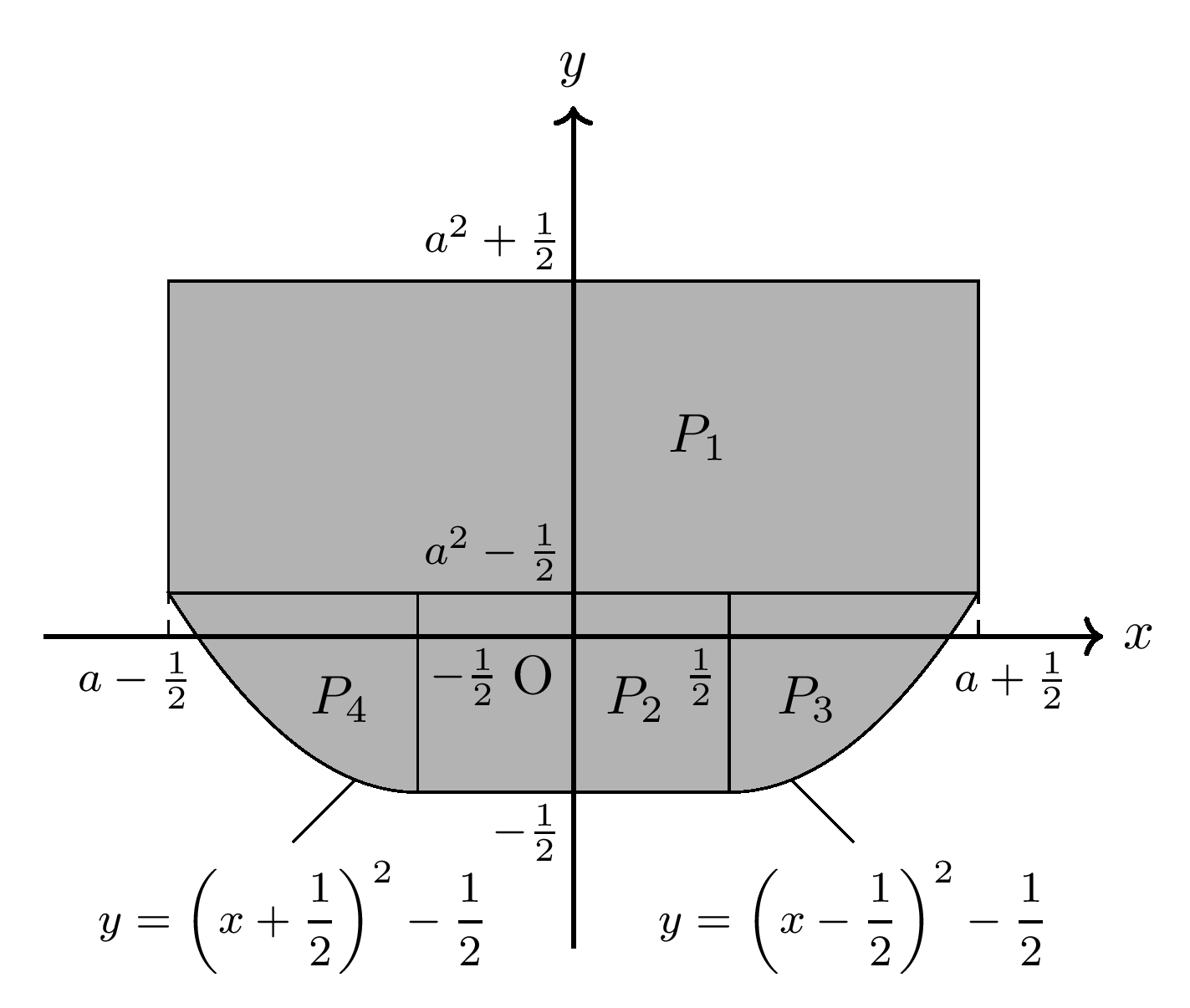
   $0\lt a\leqq \dfrac{1}{2}$のとき, $K$の通過領域は上の図のようになる.
   右の図のように, 2つの長方形部分$P_1$, $P_2$と,
   放物線と2本の直線で囲まれた図形$P_3$, $P_4$に分割でき,
   $P_3$, $P_4$は$y$軸に関して対称である.

   $P_1$は縦1, 横$\left(a+\dfrac{1}{2}\right)-\left(-a-\dfrac{1}{2}\right)=2a+1$の長方形で, 面積は$2a+1$
   $P_2$は縦$a^2-\dfrac{1}{2}-\left(-\dfrac{1}{2}\right)=a^2$, 横$\dfrac{1}{2}-\left(-\dfrac{1}{2}\right)=1$の長方形で, 面積は$a^2$
   $P_3$は放物線$y=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}$と2直線$x=\dfrac{1}{2}$, $y=a^2-\dfrac{1}{2}$によって囲まれた領域で, 面積は
   $\begin{aligned} &\dint_{\frac{1}{2}}^{a+\frac{1}{2}}\left\{a^2-\dfrac{1}{2}-\left(\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\right)\right\}dx\\ =&\dint_{\frac{1}{2}}^{a+\frac{1}{2}}\left(a^2-\dfrac{1}{4}+x-x^2\right)dx\\ =&\left(a^2-\dfrac{1}{4}\right)[x]_{\frac{1}{2}}^{a+\frac{1}{2}}+\dfrac{1}{2}[x^2]_{\frac{1}{2}}^{a+\frac{1}{2}}-\dfrac{1}{3}[x^3]_{\frac{1}{2}}^{a+\frac{1}{2}}\\ =&\left(a^2-\dfrac{1}{4}\right)a+\dfrac{1}{2}(a^2+a)-\dfrac{1}{3}\left(a^3+\dfrac{3}{2}a^2+\dfrac{3}{4}a\right)\\ =&\dfrac{2}{3}a^3+\dfrac{1}{2} \end{aligned}$

   以上より, $S(a)=2a+1+a^2+2\left(\dfrac{2}{3}a^3+\dfrac{1}{2}a\right)=\bold{\dfrac{4}{3}a^3+a^2+3a+1}$

2. 

   $\dfrac{1}{2}\lt a$のとき, $K$の通過領域は上の図のようになる.
   この面積は、(1)と同様に求められる部分($P_1$～$P_4$)の面積から,
   放物線と2本の直線に囲まれた合同な領域$P_5$, $P_6$の面積を引いたものに等しい.

   

   $P_5$は放物線$y=\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}$と直線$y=a^2+\dfrac{1}{2}$および$x$軸によって囲まれた領域で, 面積は,
   $\begin{aligned} &\dint_{0}^{a-\frac{1}{2}}\left\{a^2+\dfrac{1}{2}-\left(\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\right)\right\}dx\\ =&\dint_{0}^{a-\frac{1}{2}}\left(a^2-\dfrac{1}{4}-x-x^2\right)dx\\ =&\left(a^2-\dfrac{1}{4}\right)[x]_{0}^{a-\frac{1}{2}}-\dfrac{1}{2}[x^2]_{0}^{a-\frac{1}{2}}-\dfrac{1}{3}[x^3]_{0}^{a-\frac{1}{2}}\\ =&\left(a^2-\dfrac{1}{4}\right)\left(a-\frac{1}{2}\right)-\dfrac{1}{2}\left(a-\frac{1}{2}\right)^2-\dfrac{1}{3}\left(a-\frac{1}{2}\right)^3\\ =&\dfrac{2}{3}a^3-\dfrac{1}{2}a^2+\dfrac{1}{24}\\ \end{aligned}$

   以上より, $S(a)=\dfrac{4}{3}a^3+a^2+3a+1-2\left(\dfrac{2}{3}a^3-\dfrac{1}{2}a^2+\dfrac{1}{24}\right)=\bold{2a^2+3a+\dfrac{11}{12}}$

次回は理型第5問解説です。
文型第6問はそのさらに次回(理型第6問と同一)に解説します.

それでは、最後までお読みいただき、ありがとうございました。
ではまた。