TomoKです。
今日は「第1回垂れ流し模試」の第4問を解説します。

第4問は積分を用いた立体の体積です。
 |
| 四角形ABCDの様子(geogebraで再現) 赤:x軸 緑:y軸 青:z軸 画像はa=b=2の場合 |
回転軸である$z$軸に垂直な平面$z=0$に関して対称なので、
できる立体も、平面$z=0$に関して対称だといえます。
よって、四角形ABCDの$z\geqq 0$の部分(=△ABC)を
$z$軸の周りに回転させてできる立体の体積を$V'$とすれば、
$V=2V'$となるので、
$V'$を求めれば$V$が求められます。
さて、回転体の場合、最も基本となる公式は、
おそらく次のものでしょう。
$a<b$とする。関数$f(x)$は$a\leqq x\leqq b$で常に$f(x)\geqq 0$であるとする。
xy平面上の曲線$y=f(x)$と$x$軸, および2直線$x=a$, $x=b$とで囲まれた図形を、
$x$軸のまわして1回転させて得られる立体の体積は、
$\pi \dint_a^b \{f(t)\}^2 dt$ で与えられる。
xy平面上の曲線$y=f(x)$と$x$軸, および2直線$x=a$, $x=b$とで囲まれた図形を、
$x$軸のまわして1回転させて得られる立体の体積は、
$\pi \dint_a^b \{f(t)\}^2 dt$ で与えられる。
しかし、上の公式は、
回転軸が、回転させる図形と同じ平面に含まれていないと適用できません。
問題の立体は、平面図形の回転で得られますが、
回転軸が、回転させる図形(四角形ABCD)と同じ平面に乗っていないので、
上の公式は使えません。
ではどうするか?
この公式は特別な場合で、
一般の立体の場合には次の公式が使えます。
$a<b$とする。
$xyz$平面上にある立体$P$があるとき、
平面$x=t$ ($a\leqq t\leqq b$)による$P$の断面積が$S(t)$で与えられるとき、
$P$の$a\leqq x\leqq b$の部分の体積は
$\dint_a^b S(t) dt$で与えられる。
$xyz$平面上にある立体$P$があるとき、
平面$x=t$ ($a\leqq t\leqq b$)による$P$の断面積が$S(t)$で与えられるとき、
$P$の$a\leqq x\leqq b$の部分の体積は
$\dint_a^b S(t) dt$で与えられる。
上の青網掛けの公式は、
この赤網掛けで$S(t)=\pi\{f(t)\}^2$とすることで
得られる公式だったのでした。
今回はこの赤網掛けを利用します。
ということは断面を考えればよいわけですが、
今回は図形を$z$軸の周りに1回転しているので、
断面は$z$軸に垂直な、平面$z=t$による断面を考えるといいでしょう。
ただし、$z\geqq 0$の部分の体積$V'$を求める場合
$z$方向の最上点がB, 最下点がAおよびCであることから、
$t$の範囲は$0\leqq t\leqq 2b$となります。
さて、平面$z=t$による立体の断面は、
平面$z=t$による四角形ABCDの断面を考えて、
それを、中心となる$z$軸を中心に回転させた図形を考えればいいでしょう。
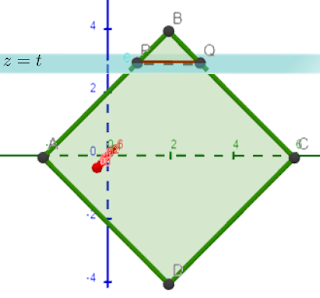 |
| 四角形ABCDと平面z=tとの交差部分は線分 |
上の図でいう線分PQになるはずです。
ここで、PはAB上の$z=t$となる点であり、
ABは$x=a$, $z=y+b$となる直線なので、
($y$軸と$z$軸を四角形ABCDに平行移動してみるとわかりやすい)
Pの$y$座標は$t-b$です。
同じように、QはBC上の$z=t$となる点で、
BCは$x=a$, $z=-y+3b$となる直線なので、
Qの$y$座標は$3b-t$です。
以上から、線分PQは平面$z=t$上で、
直線$x=a$の$t-b\leqq x\leqq 3b-t$の部分(線分)
にあたることがわかり、
これが四角形ABCDの平面$z=t$による断面になります。
この線分PQを、$z$軸との交点であるO'$(0,0,t)$に関して回転させれば、
問題の立体の平面$z=t$による断面が得られます。
すると、立体の平面$z=t$による断面は、
O'を中心に、「そこからの距離が最大になる線分PQ上の点」を通る円(内部および周)
から
O'を中心に、「そこからの距離が最小になる線分PQ上の点」を通る円の内部
を除いたもの
になることがわかります。
さて、これで断面積$S(t)$を考えればよいのですが、
実は$S(t)$は$t=b$を境に状況が分かれます。
(i) $0\leqq t\leqq b$のとき
 |
| 四角形ABCDを平面z=tで切断した時の断面(0≦t≦b) |
最小なのは、O'からPQに下した垂線の足H$(a,0,t)$
${\rm O'Q}=\sqrt{a^2+(3b-t)^2}$, ${\rm O'H}=a$より、
$S(t)=\pi \left(\sqrt{a^2+(3b-t)^2}\right)^2-\pi a^2=\pi (3b-t)^2$
 |
| できる立体を平面z=tで切断した時の断面(0≦t≦b) |
(ii) $b\leqq t\leqq 2b$のとき
 |
| 四角形ABCDを平面z=tで切断した時の断面(b≦t≦2b) |
最小なのは、P$(a,t-b,t)$
${\rm O'Q}=\sqrt{a^2+(3b-t)^2}$, ${\rm O'P}=\sqrt{a^2+(t-b)^2}$より、
$\begin{aligned}
S(t)=&\pi \left(\sqrt{a^2+(3b-t)^2}\right)^2-\pi \left(\sqrt{a^2+(t-b)^2}\right)^2\\
&=\pi (9b^2-6bt+t^2-t^2+2bt-b^2)\\
&=4\pi b(2b-t)
\end{aligned}$
 |
| できる立体を平面z=tで切断した時の断面(b≦t≦2b) |
後は積分するだけです。
問題の立体の$z\geqq 0$の部分の体積$V'$は、
$\begin{aligned}
V'&=\dint_0^{2b}S(t) dt=\pi\dint_0^b(3b-t)^2 dt+4\pi b\dint_b^{2b}(2b-t) dt\\
&=\pi\left\{-\dfrac{1}{3}{\big[(3b-t)^3\big]}_0^b-2b{\big[(2b-t)^2\big]}_b^{2b}\right\}\\
&=\pi\left(-\dfrac{8b^3}{3}+9b^3+2b^3\right)=\dfrac{25}{3}\pi b^3
\end{aligned}$
です。
よって、求める立体の体積$V$は、
最初の対称性の話で書いた通り$V=2V'$ですから、
$V=2\cdot \dfrac{25}{3}\pi b^3=\bold{\dfrac{50}{3}\pi b^3}$
となります。
ちなみに、できる立体は下のようになります。


左が横から見た図で、右が斜め上の角度から見た図です。
できる立体は、外側が双曲面で、
内側の穴は中心付近が円柱、上下の穴の入り口も双曲面になっています。
一般に、直線を、それに垂直でないねじれの位置にある直線の周りに
1回転させると、双曲線を回転させてできる曲面(双曲面)ができます。
今回は四角形の各辺が回転軸にねじれているので、
全体的に双曲面が多い図形になっているわけですね。
このような、断面積を積分して体積を求める問題は、
入試でも毎年どこかの大学で出題されています。
難関大でも出ることはありますし、
簡単なものは中堅大学で出題されることもあるので、
チェックしておきたいところですね。
といったところで、第4問の解説はここまでです。
次回は第5問解説です。
最後までお読みいただき、ありがとうございました。
ではまた!
0 件のコメント:
コメントを投稿