【回顧】第2回垂れ流し数学模試 第5問解説

皆さんこんにちは!
TomoKです。

この記事では、第2回垂れ流し数学模試の第5問を解説します。

第5問

第5問は積分を応用した体積の計算です。
図を描いてみるとわかると思いますが、PとQの共通部分は、
下の図のようにPより高さが小さい円柱の上下に、
Qの一部分がふたのようにくっついた形になります。

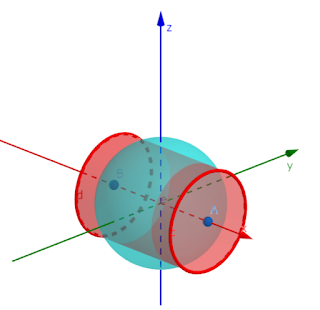直円柱Pと球Q　(GeoＧebraで作成) 

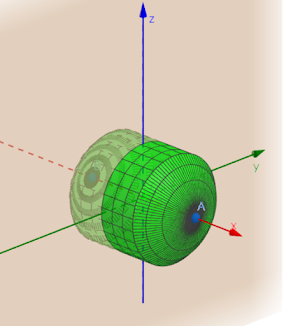直円柱Pと球Qの共通部分R (GeoGebraで作成)
茶色いのはyz平面

そこで、円柱部分はすぐ体積が分かるとして、
上下にくっついたQの一部分の体積を積分で求めます。

解答例



解答例では対称性を用いて合同な上下2つの立体に分けた後に、
その高さに当たる方向に$x$軸をとっています。

円柱と「ふた」の境目を三平方の定理を用いて求めると、
$x=\dfrac{3}{2}r$となります。
つまり$\dfrac{3}{2}r$から$\dfrac{3}{2}r$まではQの一部である「ふた」で、
この部分で$x$に垂直な断面の面積を求めていきます。

平面$x=t$で切ったときの断面積も、三平方の定理を援用すればすぐに求められますので、
あとは 積分→Pの上部分をたす→対称性から2倍 の形で計算すればOKです。

球を平面で切った一部分を求める問題は、過去に筑波大で、
「半球型の容器を水で満たして傾けた時、残った水の体積を求める」
という形で出題されたことがあります。
球を平面で切った一部分の体積は割と基本的な問題ですので、
計算ミスに注意しつつ確実に解けるようにしてほしいところです。

次の記事は第2回垂れ流し数学模試の第6問、いよいよ最後の問題です。

ここまでお読みいただき、ありがとうございました。

ではまた!