実に1週間ぶりの更新でした…
私もやることがいろいろとあって
全く暇だというわけではないので…
まあ、この季節は引っ越しとやら入学・就職とやらで
忙しい方も多いでしょう。
皆様はいかがだったでしょうか?
さて、前回は、中学校の因数分解の復習をやりました。
今回こそは、新しい因数分解の手法を
皆さんに伝授することができると思います。
今日はその手法に慣れてもらいたいと思っています。
今までは、主に2次式でも、
2乗の項の係数が1であるものが基本でしたが、
今回学習するのは
2乗の項の係数が1ではない2次式も因数分解できる場合があるよ!
ということがわかると思います。
では、今回のお話を始めます。
[1] 2次式の因数分解(たすき掛け)
公式5(の逆) $\blue{ac}x^2+(\orange{ad+bc})x+\green{bd}=(ax+b)(cx+d)$
これを使うと、冒頭でお話しした
「2乗の項の係数が1でない2次式」は、
因数分解されやすくなります。
例えば、
$\blue{6}x^2+\orange{17}x+\green{5}$を因数分解したいと思います。
上の公式5と比較してください。
$\blue{ac=6}, \orange{ad+bc=17}, \green{bd=5}$
ということがわかるので、
これら3つを満たす4つの整数$a,b,c,d$を見つければ、
因数分解が成功するわけです。
コツとしては、$x^2$の項の係数が1のときと同様に
"積"から"和"の順番で決めていきます。
しかし、今回は"積"が2つありますので、
"積"$\blue{ac=6}, \green{bd=5}$となるような$a,b,c,d$の候補のうち、
$\orange{ad+bc=17}$となるものをとればよい、
ということになります。
 |
| たすき掛け |
これを図式化したのが、
右の「たすき掛け」と呼ばれる、
縦3列、横3列を使う筆算みたいな因数分解の方法です。
ここでは、
$\blue{6}x^2+\orange{17}x+\green{5}$
の因数分解を例に、「たすき掛け」を説明したいと思います。
①最も下の横列に、
 |
| ①下の横列に係数を書く。真ん中は最後 |
数を書き入れます。
順番注意! 真ん中だけ最後、と覚えておきましょう。
今回は$\blue{6},\green{5},\orange{17}$と
数を入れておくわけですね。
 |
| ②左の縦列。積が6になるような2つの数を書く。 |
②最も左の縦列の、上から1つ目と2つ目に
かけて6になる2つの整数を入れます。
ためしに$2,3$と入れてみましょう。
 |
| ③中央の縦列。積が5になるような2つの数を書く。 |
③真ん中の縦列の、上から1つ目と2つ目に
かけて5となる2つの整数を入れます。
こちらもとりあえず$1,5$と入れておきましょうか。
④ななめどうしをかけて
最も右の縦列の、上から1つ目と2つ目に 記入します。
そして、記入した2つの数を足して、
 |
| ④ななめどうしかけて右の縦列に。 それらを足しても下の数字17に合わない。 |
今回の場合は、
$3\times 1=3$より、1つ目は$3$
$2\times 5=10$より、2つ目は$10$です。
そして、今記入した2つの数を足しますと、
$3+10=13$となります。
しかし、下の数字は17ですから、
今回は残念ながら失敗です...
⑤もし④で下の数字に一致しなければ、
③に戻って、真ん中の縦列に入れる数を変えます。
もし、いくら真ん中を変えても一致しないようであれば、
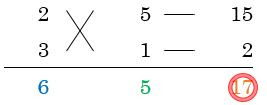 |
| ⑤真ん中の縦列を変えてみた。 再びななめをかけてから足すと17で一致 $6x^2+17x+5=(2x+5)(3x+1)$ |
ここら辺は試行錯誤するしかありません。
今回は、真ん中を$5,1$とすると、
$3\times 5=15$
$2\times 1=2$
を右の縦列に書き入れて、
$15+2=\orange{17}$と一致します。
これでめでたく成功です!
⑥あとは、上の横列の左から2つ、
真ん中の横列の左から2つを見て、
係数を書いていけば終わりです。
$\underline{6x^2+17x+5=(2x+5)(3x+1)}$というわけですね。
この「たすき掛け」を使うと、
因数分解できる2次式は、
すべて因数分解できるようになります。
…まあ途中の数字のあてはめが、この「たすき掛け」のヤマなんですがね…
慣れるために、別の問題でやってみましょうか。
例題
EXQ1. 次の式を因数分解せよ。
(1) $4x^2+8x-5$ (2) $10x^2-19x+6$ (3) $8x^2-13xy-6y^2$
EXQ1. 次の式を因数分解せよ。
(1) $4x^2+8x-5$ (2) $10x^2-19x+6$ (3) $8x^2-13xy-6y^2$
これらも「たすき掛け」をうまく使えば
ちゃんと因数分解できます。
上の方法にならって、
自分の手でやってみてください。
最初下の横列に書く順番は
真ん中($x$の項)が最後です!
また、記入する数字が負の数(マイナス)になることがあるので、
探し忘れたり、マイナス(-)をつけ忘れたり、
かけたり足したりするときに
符号を間違えたりないようにしましょう。
どうでしょうか?
まず(1)を、手順に沿ってやってみると、
下のようになるかと思います。
この図だとあたかも一発でできてるように見えるかもしれませんが、
実際のところは②~④で何度か数字を書き直して
正しいものを見つけていけばいいですよ!

ということで、
答えは$\boldsymbol{4x^2+8x-5=(2x-1)(2x+5)}$となります。
 この調子で(2)や(3)をやると、
この調子で(2)や(3)をやると、「たすき掛け」の結果は右のようになります。
(2)は
$\boldsymbol{10x^2-19x+6=(2x-3)(5x-2)}$
となります。
(3)は、もう1つの文字$y$を忘れないようにして
$\boldsymbol{8x^2-13xy-6y^2=(x-2y)(8x+3y)}$
となります。
では、今度の2次式はどうでしょうか?
$\blue{4}x^2\orange{-12}x+\green{9}$
 |
| $4x^2-12x+9$の「たすき掛け」 |
もちろん! これも「たすき掛け」で因数分解できます。
「たすき掛け」を使うと、右の図のようになります。
したがって、
$4x^2-12x+9=(2x-3)(2x-3)=(2x-3)^2$
となります。
ん? ${}^2$が出たということは!?
そうです。
実はこの場合は、公式3(3')を使えるんですね。
$4x^2-12x+9=(\red{2x})^2-2\cdot \red{2x}\cdot \blue{3}+\blue{3}^2=(\red{2x}-\blue{3})^2$
両端の項が2乗の形にかけるとき、
場合によっては中央の項を見極めるだけで(2×両端の2乗をとったものの積)
因数分解できることがあります。
そうなってないときは、仕方なくたすき掛けします。
あともう1つ。
$25x^2-64$
これは2乗の差、公式4です。
$25x^2-64=(\red{5x})^2-\blue{8}^2=(\red{5x}+\blue{8})(\red{5x}-\blue{8})$
このパターンのときはずいぶん楽ですね。
いずれにしても、
因数分解のときには、
まず式の形を見極めて、どの手法を使えばいいかを
冷静に判断するわけですね。
では、練習問題です。
すべて「たすき掛け」を使えば解ける問題です。
練習問題
Q1. 次の式を因数分解せよ。 [解答]
(1) $2x^2+3x+1$ (2) $3x^2-x-2$ (3) $7x^2+10x-8$
(4) $6a^2-11a+3$ (5) $12x^2-11x-15$ (6) $9x^2+6x+1$
(7) $4x^2-20x+25$ (8) $9x^2-49$ (9) $16x^2-30xy+9y^2$
(10) $18x^2+xy-4y^2$ (11) $16a^2+24ab+9b^2$ (12) $4x^2-81y^2$
Q1. 次の式を因数分解せよ。 [解答]
(1) $2x^2+3x+1$ (2) $3x^2-x-2$ (3) $7x^2+10x-8$
(4) $6a^2-11a+3$ (5) $12x^2-11x-15$ (6) $9x^2+6x+1$
(7) $4x^2-20x+25$ (8) $9x^2-49$ (9) $16x^2-30xy+9y^2$
(10) $18x^2+xy-4y^2$ (11) $16a^2+24ab+9b^2$ (12) $4x^2-81y^2$
[2] 3次式の因数分解(公式の逆パターン)
さて、2次式についての因数分解の
基本的なところは終わりました。
今度は3次式、といきたいところですが、
3次以上の式の因数分解は、
一般的には少し困難なことが多いです。
(後日登場する「因数定理」を使うと
ある程度楽になりますが…)
しかし、公式を使える場合であれば
すぐに因数分解できます。
公式7(の逆) $\green{a}^{3}\red{+3}\green{a}^{2}\blue{b}\red{+3}\green{a}\blue{b}^2\red{+}\blue{b}^3=(\green{a}\red{+}\blue{b})^3$
公式7'(の逆) $\green{a}^{3}\red{-3}\green{a}^{2}\blue{b}\red{+3}\green{a}\blue{b}^2\red{-}\blue{b}^3=(\green{a}\red{-}\blue{b})^3$
注意すべきは、まず
・両端が3乗
ということです。
次に、展開のときの注意と同じく、
・左からaが3次から次数を減らしていき、3→2→1→0と変化
・左からbが0次から次数を増やしていき、0→1→2→3と変化
・中2つのところに係数3がつく
です、また、
・()の中の符号は全部+なら+、交互に+-なら-
です。
例えば、
$27x^3+27x^2+9x+1$
は$27x^3=(\green{3x})^3, 1=\blue{1}^3$で、
さらに上のことをチェックすると、
$\begin{align*}
27x^3+27x^2+9x+1&=(\green{3x})^{3}\red{+3}\cdot \green{3x}^{2}\cdot \blue{1}\red{+3}\cdot \green{3x}\cdot \blue{1}^2\red{+}\blue{1}^3\\
&=(\green{3x}\red{+}\blue{1})^3
\end{align*}$
となります。
また、
$x^3-6x^{2}y+12xy^2-8y^3$は、
これも上のことをチェックすると、
$\begin{align*}
x^3-6x^{2}y+12xy^2-8y^3&=\green{x}^{3}\red{-3}\cdot \green{x}^{2}\cdot \blue{2y}\red{+3}\cdot \green{x}\cdot (\blue{2y})^2\red{-}(\blue{2y})^3\\
&=(\green{x}\red{-}\blue{2y})^3
\end{align*}$
となります。
公式通りにあてはめられるかを
丁寧にチェックしましょう。
最後にこの公式。
公式8(の逆) $\green{a}^3\red{+}\blue{b}^3=(\green{a}\red{+}\blue{b})(\green{a}^2\red{-}\green{a}\blue{b}\red{+}\blue{b}^2)$
公式8'(の逆) $\green{a}^3\red{-}\blue{b}^3=(\green{a}\red{-}\blue{b})(\green{a}^2\red{+}\green{a}\blue{b}\red{+}\blue{b}^2)$
3乗+3乗, 3乗-3乗のときの公式ですが、
・最初の( )はそのままの符号
・次の( )は、真ん中は逆符号(2はつかない)、最後は+
と覚えます。
例えば$x^3+8$はこの公式の形ですね。
$\begin{align*}
x^3+8=\green{x}^3\red{+}\blue{2}^3&=(\green{x}\red{+}\blue{2})(\green{x}^2\red{-}\green{x}\cdot \blue{2}\red{+}\blue{2}^2)\\
&=(x+2)(x^2-2x+4)
\end{align*}$
と因数分解できます。
また、$27x^3-64y^3$は、
$\begin{align*}
27x^3-64y^3&=(\green{3x})^3\red{-}(\blue{4y})^3=(\green{3x}\red{-}\blue{4y})\{(\green{3x})^2\red{+}\green{3x}\cdot \blue{4y}\red{+}(\blue{4y})^2\}\\
&=(3x-4y)(9x^2+12xy+16y^2)
\end{align*}$
となりますね。
お疲れ様でした…
公式を利用する因数分解はここまでです。
次回は、より工夫した因数分解の手法をお話しできたらと思います。
それまでに、今回と前回の内容をきっちり押さえておきましょう!
では、今回はここまで。
お読みくださりありがとうございました。
ではまた!
--------------------
練習問題の答え
Q1. (1) $(x+1)(2x+1)$ (2) $(x-1)(3x+2)$ (3) $(x+2)(7x-4)$
(4) $(2a-3)(3a-1)$ (5) $(3x-5)(4x+3)$ (6) $(3x+1)^2$
(7) $(2x-5)^2$ (8) $(3x+7)(3x-7)$ (9) $(2x-3y)(8x-3y)$
(10) $(2x+y)(9x-4y)$ (11) $(4a+3b)^2$ (12) $(2x+9y)(2x-9y)$
Q2. (1) $(x-4)^3$ (2) $(2x+3y)^3$
Q3. (1) $(4x-1)(16x^2+4x+1)$ (2) $(2a+3b)(4a^2-6ab+9b^2)$
0 件のコメント:
コメントを投稿